【疑問】1日で「ボーナス100回」引けるのか？

スロットで真面目に稼ぐ人には、ジャグやハナの設定6を1日で万回転回す人がいます。
(私には真似できません)
一方でスロッターの夢として「1日にボーナスを100回引きたい」と考えたことはありませんか？

スロットは確率との戦い、ボーナスが確率よりつく日もつかない日もあります。
ボーナス100回達成には相当のつきが必要です。
その確率は、一体どのくらいでしょうか。





…ガチで計算してみました。



[問題]
通常時10000回転にてボーナス100回を達成できる確率を、統計学を用いて求めよ。
ただし検証機種は、マイジャグラーV設定6(合算1/114.6)とする。

[結論]
8.53%、つまり万回転の11.73回に1回達成できる。


[ざっくり用語解説]
試行回数
乱数抽選をする回数のことで、今回は通常時回転数を指す。
以降、本解説では試行回数をn(=10000)と定義する。

当選確率
ある事象が成功する確率で、今回はボーナス当選率を指す。
以降、本解説では当選確率をp(=1/114.6)と定義する。
また当選しない確率をq=1-pと定義する。

二項分布
ボーナス抽選をn回試行したとき、ボーナス当選回数が取る確率分布をいう。
以降、この分布をP(X)と定義する。ここでXはボーナス当選回数を指す。
Xを決めたとき、P(X)は万回転でボーナスがX回当たる確率となる。

期待値
ボーナスを確率通り引いたとき、ボーナスが当選する回数をいう。
以降、期待値をμ=n×pと定義する。

分散
確率の分布を示す統計量。
要はボーナス出現回数の荒れ模様を指す指標である。以降、分散をρと定義する。
二項分布においては、ρ=n×p×qと計算できる。
(※導出はかなり面倒なため省略)

標準偏差
分散の平方根(ルート)を取ったもの。以降、標準偏差をσ(=√ρ)と定義する
二項分布や正規分布における期待値からの離れ方の指標である。
今回の出現率計算におけるカギを握る。

正規分布
統計学において最も標準的に活用される確率分布。
先述の二項分布は「n×pが十分大きいとき、正規分布で近似できる」という定理がある。
そのため、今回の確率計算は最終的に正規分布を用いる。今回の計算の主役だ。
正規分布のグラフはこんな感じ。決して男のテントではない。

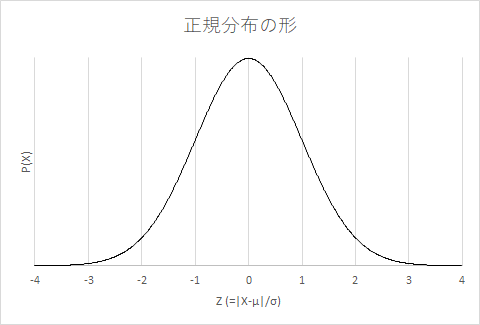
[計算方法]
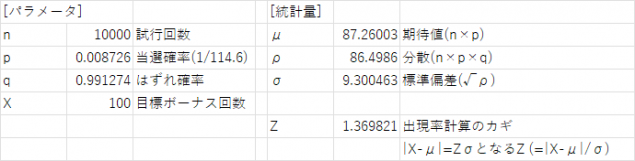
まずは用語解説で述べた、期待値：μ、分散：ρ、標準偏差：σを定義通り計算する。
この値を用いて、出現率計算のカギ：Z=|X-μ|/σを求める。

ここで計算したZを使うと、正規分布において黄塗りした部分が出現する確率が求められる。
つまり今回の場合だと、ボーナス回数が87.2～100回までの間に収まる確率が計算できる。
正規分布における確率の計算には、「標準正規分布表」というZが決まると確率が出てくる便利道具が使える。
今回はZ≒1.37となり、当該確率は0.4147と算出される。

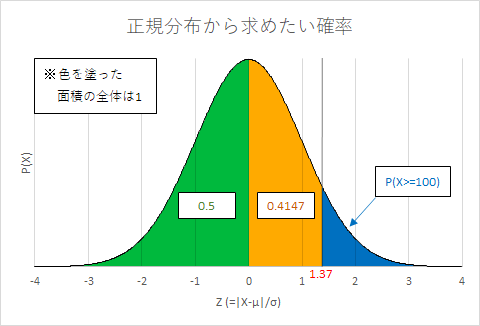
今回求める確率は図の青塗り部分で、ボーナスが期待値：μ回以上引けない確率は0.5である。
(裏を返せば、ボーナスが期待値：μ回以上引ける確率も0.5である。)
以上より今回求めたい確率：P(X>=100)は、下記により求められる。
P(X>=100) = 1-(0.5+0.4147) = 0.0853



…8.53%、こうやって聞くと実現できちゃいそうですよね。夢があります。
やはり問題は設定6をツモれること、体力・精神力の問題で万回転回せること、でしょうか。


ところで今回使用した数学のレベル、どれくらいかと言いますと…。
調べたところ正規分布自体は高校数学における「数学B」にて取り扱われる品物だそうです。
ただここまで実用的に計算するには、理系に所属する鍛えられた高校生か、大学生以上かという所ですかね？

次回はこの計算手法を用いて、パチスロの検定がどれだけギリギリを攻めてるかを検証したいと思います。(続くのか！？)

12